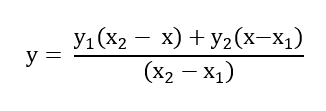You are given the X, Y Coordinates of 2 points, (99.5,39.5) and (201.1,45.7) and asked to find the Y coordinate of an intermediate point with an X coordinate of 115.7. How will you solve this problem?
The answer is Interpolation!
Interpolation is the method of estimating ‘unknown values’ that fall between ‘known values’.
In this blog post, I will explain 2 Excel formulas to perform Linear interpolation to find the unknown.
Table of Contents
Linear Interpolation Formula
If there are 2 known points denoted by the coordinates (x1, y1) and (x2 y2), the y coordinate of x in between x1 and x2 can be found out by the following formula
See the following problem. If x1 = 99.5, y1 = 39.5, x2 = 201.1 and y2 = 45.7, what is the y coordinate of the point with x coordinate,115.7?
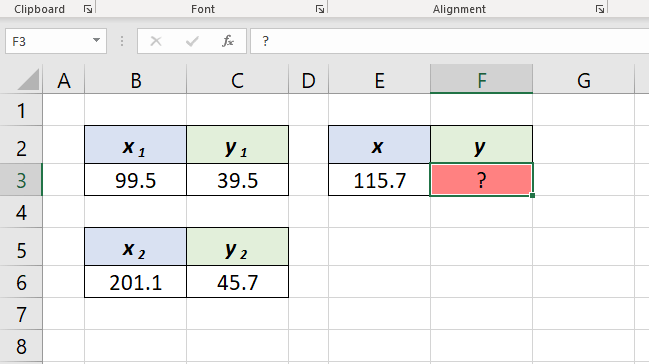
When the above values are supplied into the Linear Interpolation formula, the formula to find the y coordinate will become,
=(39.5*(201.1-115.7)+45.7*(115.7-99.5))/(201.1-99.5)
In our Excel worksheet, x1 is in B3, y1 in C3, x2 in B6, y2 in C6 and x is in E3. So, the Excel formula equivalent to the above formula is,
=(C3*(B6-E3)+C6*(E3-B3))/(B6-B3)
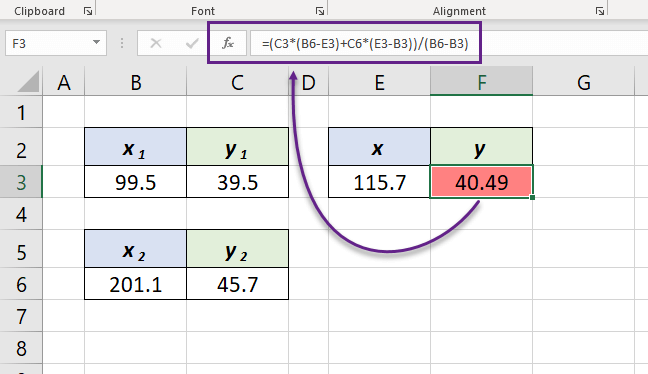
and the formula evaluates to 40.49.
Interpolation with FORECAST.LINEAR function
FORECAST.LINEAR function in Excel is used to predict a linear trend based on known values and the same can be used to perform Interpolation.
Let’s solve the same problem that we discussed above, using FORECAST.LINEAR function.
x1 = 99.5 (B3), y1 = 39.5 (C3), x2 = 201.1 (B4), y2 = 45.7 (C4) and we need to find the y when x = 115.7 (E3)
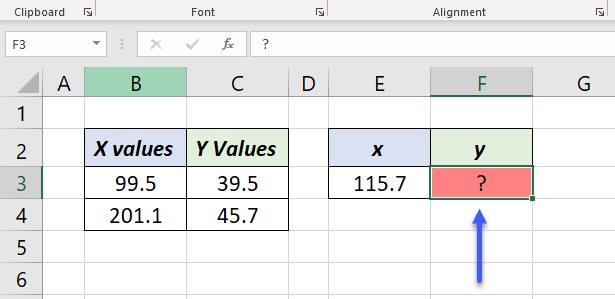
FORECAST.LINEAR has 3 arguments x, known_ys, and known_xs.
Here, x is 115.7, the value in the cell E3.
known_ys are 39.5 and 45.7, the values in the cells C3 and C4.
known_xs are 99.5 and 201.1, the values in the cells B3 and B4.
So, the formula to calculate y value is,
=FORECAST.LINEAR(E3,C3:C4,B3:B4)
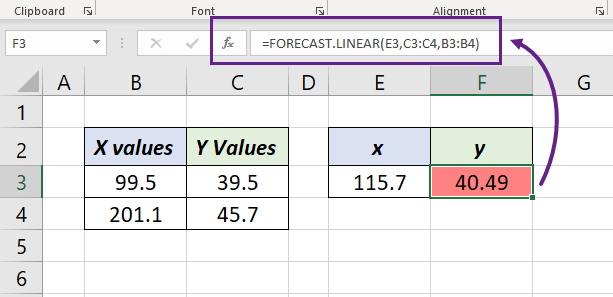
and the formula will return 40.49.
Calculating Y values against X values at regular intervals
Following is another problem where we need to find the Y values against X values at 10-meter intervals (Column E).
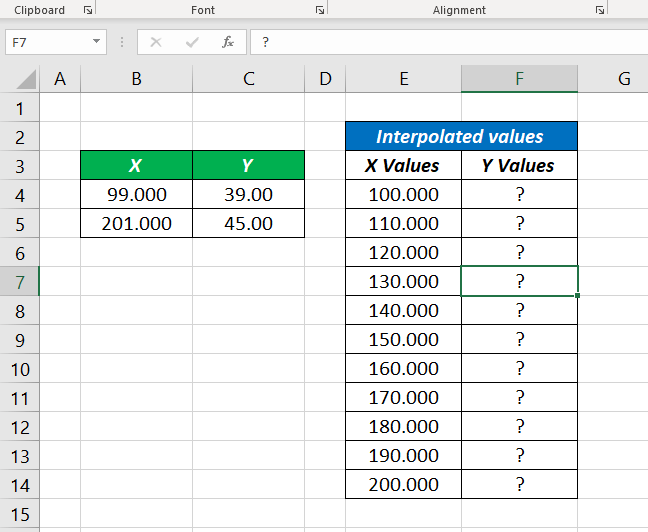
Method 1
Solution using Linear Interpolation Formula.
We have x1 in B4, y1 in C4, x2 in B5, y2 in C5 and x in E4
Linear Interpolation formula to find the Y coordinate against the X coordinates value in E4 (100) is,
=(((C5-C4)/(B5-B4))*(E4-B4))+C4
After locking the required cell references, the same formula can be copied into the adjacent cells below to calculate the Y coordinates for the remaining X values.
=((($C$5-$C$4)/($B$5-$B$4))*(E4-$B$4))+$C$4
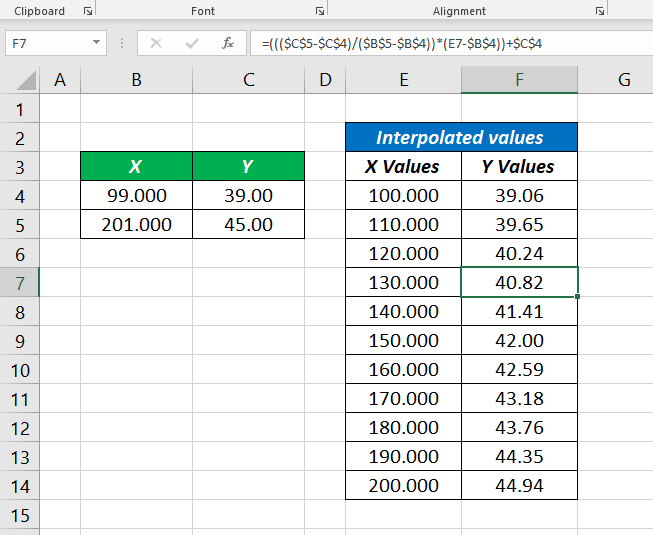
Method 2
The same problem solved using FORECAST.LINEAR function.
We have x1 is in B4, y1 in C4, x2 in B5, y2 in C5 and x in E4

Formula to find the Y coordinate against the X coordinates value in E4 (100) is,
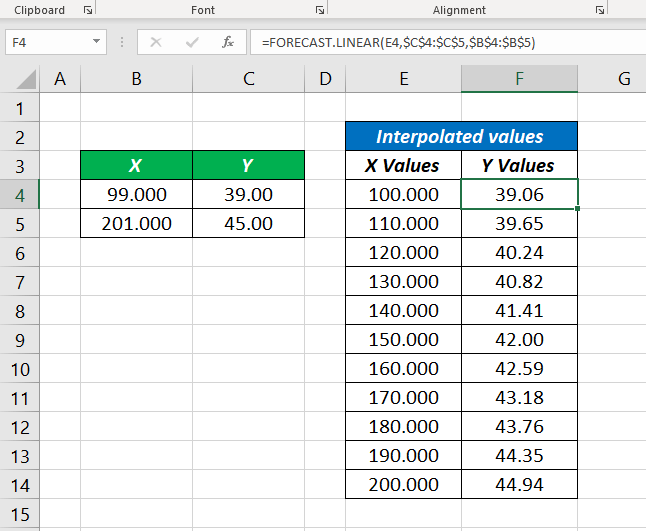
=FORECAST.LINEAR(E4,C4:C5,B4:B5)
After locking the required cell references, the same formula can be copied into the adjacent cells below to calculate the Y coordinates for the remaining X values.
=FORECAST.LINEAR(E4,$C$4:$C$5,$B$4:$B$5)
Excel Functions in Alphabetical Order (Complete list)
Complete List of Excel Functions (Category wise)